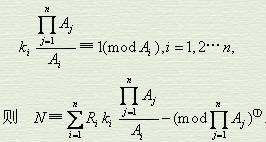Chapter 46 Section 4: The Summarization Technique of Dayan and the Technique of Finding One in Dayan

Chinese folks have always circulated number games such as "King Qin's Dark Pointing Soldiers", "Han Xin Pointing Soldiers", "Ghost Valley Calculation", "Partition Wall Calculation", and "Cutting Pipe Technique". "Sun Tzu Suan Jing" asked "things do not know how to count", Qin Jiushao called it "Da Yan's total number technique", which is the solution method of the first-order congruence formula.Congruence is an important concept in number theory. Given a positive integer m, if two integers a and b make ab divisible by m, it is said that a and b are congruent to modulo m, recorded as a≡b(mod m) . The question of "I don't know the number of things" is: "Today there are things that don't know the number. The number of three and three leaves two, the number of five and five leaves three, and the number of seven and seven leaves two. Ask the geometry of things?" This is the first time in the history of world mathematics that congruent formula problem.Expressed in modern symbols, this question is to find the smallest positive integer N that satisfies the congruence formula: N≡2(mod 3)≡3(mod 5)≡2(mod 7). The solution of "Sun Tzu's Mathematical Classics" is

N=2×70+3×21+2×15-2×105=23. The basis is: 70=2×5×7≡1 (mod 3), 21=3×7≡1 (mod 5), 15=3×5≡1 (mod 7).It can be seen that the author of "Sun Tzu's Mathematical Classics" understood the following theorem to a certain extent: If Ai (i=1, 2...) is a pairwise prime positive integer, Ri<Ai, Ri is also a positive integer (i=1, 2...), and the positive integer N satisfies the congruence group N≡Ri(mod Ai)i=1, 2... If you can find all positive integers ki, make Euler (AD 1707-1783), the masters of modern European mathematics, and Lagrange (AD 1736-1813) have both done research on congruence problems.Gauss (AD 1777-1855) wrote the above theorem explicitly in Inquiry Arithmetic (AD 1801).In 1852, the missionary to China, Weilie Yali (AD 1815-1887), introduced the problem of "things don't know how many things" to the West. People found that it was consistent with the above theorem, so they called it the Chinese remainder theorem.

The congruence solution method also comes from the calculation of the cumulative years of the Shangyuan in the formulation of the calendar.The ancient Chinese calendar assumes that there was a Jiazi day in ancient times, and the winter solstice of that year and the Heshuo of November both happened to be at the beginning of this day.The year with such a day is called Shangyuan, and the total number of years from Shangyuan to the current year when the calendar is formulated is called Shangyuan accumulated years.Knowing the time of the winter solstice this year and the time of Pingshuo in November, finding the "Shangyuan Jinian" is a problem of congruence in mathematics.However, "Although the historians use it, they don't know it" ("Nine Chapters of Shushu"), it was the Southern Song mathematician Qin Jiushao who first proposed a complete solution of a congruence group in the history of Chinese mathematics and the history of world mathematics.

Qin Jiushao's method is called Dayan Total Number Technique.He called the ki multiplication ratios, and the Ai definite numbers, , q...the remainders are r, r...according to certain rules, c and c are calculated in the lower left and upper left...until the upper right rn=1 (at this time n must is an even number), then c=qc+c on the upper left is the value of k to be sought.In modern notation it is: Here it is necessary to calculate to the upper right rn=1, so it has the name of "seeking one".It can be proved that this method of multiplying the rate k is correct.In the above method, all Ai must be positive integers that are mutually prime, but in practical problems, all Ai are not necessarily mutually prime, or even integers, and may be fractions or decimals.According to different situations, Qin Jiushao proposed a procedure to reduce various problems into definite numbers.Since there was no concept of factorization in ancient China, the reduction process took a detour, but after all, it solved this problem relatively successfully.

Qin Jiushao not only used the Dayan total number method for calendar calculations, but also for construction, itinerary, corn transactions, interest on treasury amounts, and even case resolution.I would like to take the question of "Yu Mi Tui Shu" as an example.A rice shop complained that three baskets of rice had been stolen, but the quantity was unknown.There is 1 round left in the left basket, 14 rounds left in the middle basket, and 1 round left in the right basket.Later, the rice thieves A, B, and C were caught.A said that he found a horse ladle that night, and scooped the rice from the left ladle into the cloth bag one by one; B said that he kicked a wooden shoe and scooped the rice from the middle basket into the cloth bag; Just paint the bowl and scoop the rice from the right basket into the cloth bag.The three of them took the rice home and ate it. After a long time, they didn't know the number, so they handed over the tools for committing the crime.The volume of a horse ladle is 19, a wooden shoe is 17, and a lacquer bowl is 12.Ask the total number of meters lost and the number of meters stolen by the three people.This is the solution N of the congruence system.

N≡1(mod 19)≡14(mod 17)≡1(mod 12) Since 19, 17, and 12 are mutually prime, they are definite numbers.The parent is 19×17×12=3876, and the number of derivatives is 17×12=204, 19×12=228, and 19×17=323.Find the multiplication factors k, k, and k that satisfy k×204≡1 (mod 19), k×228≡1 (mod 17), and k×323≡1 (mod 12), respectively.Since the derived numbers are respectively greater than the fixed numbers, the fixed numbers are used to subtract the derived numbers to obtain odd numbers 14, 7, and 11.The problem becomes to find k, k, k that satisfy k×14≡1 (mod 19), k×7≡1 (mod 17), k×11≡1 (mod 12), respectively.The program for finding k:

The program for finding k: 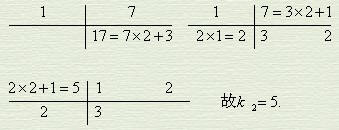The program for finding k: So N≡1×15×204+14×5×228+1×11×323(mod 3876)≡22573(mod 3876)=3193. The number of rice per basket is 3193, A and C each steal 3192, and B steals 3179, for a total of 9563.

---

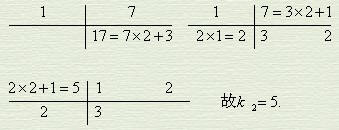
Notes: a=aaa...a